Build Long-term Wealth
Enjoy higher returns from your investments
Enjoy Peace of Mind
Remain stress-free as you invest
with India's largest Investment Advisor
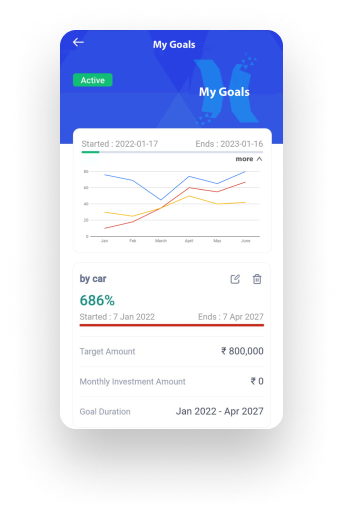
Achieve your Financial Goals
Watch your investments bloom while
you focus on living the life of choice.
Enjoy higher returns from your investments
Remain stress-free as you invest
with India's largest Investment Advisor
Watch your investments bloom while
you focus on living the life of choice.

Experience Exceptional Long-term Performance With Our Acclaimed AI-powered Research
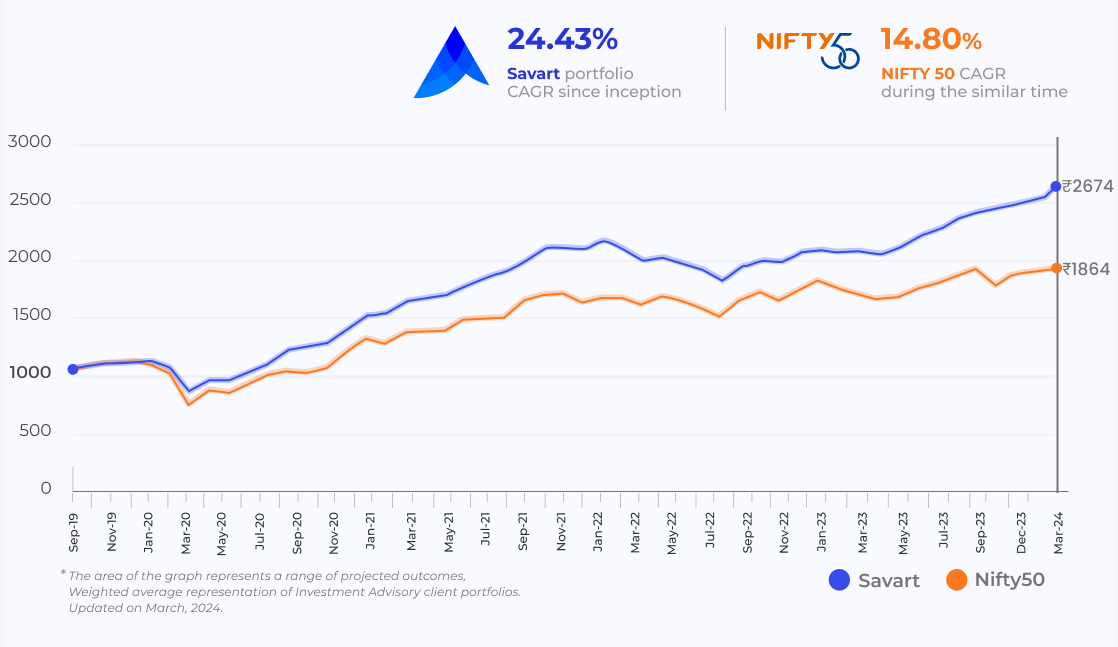
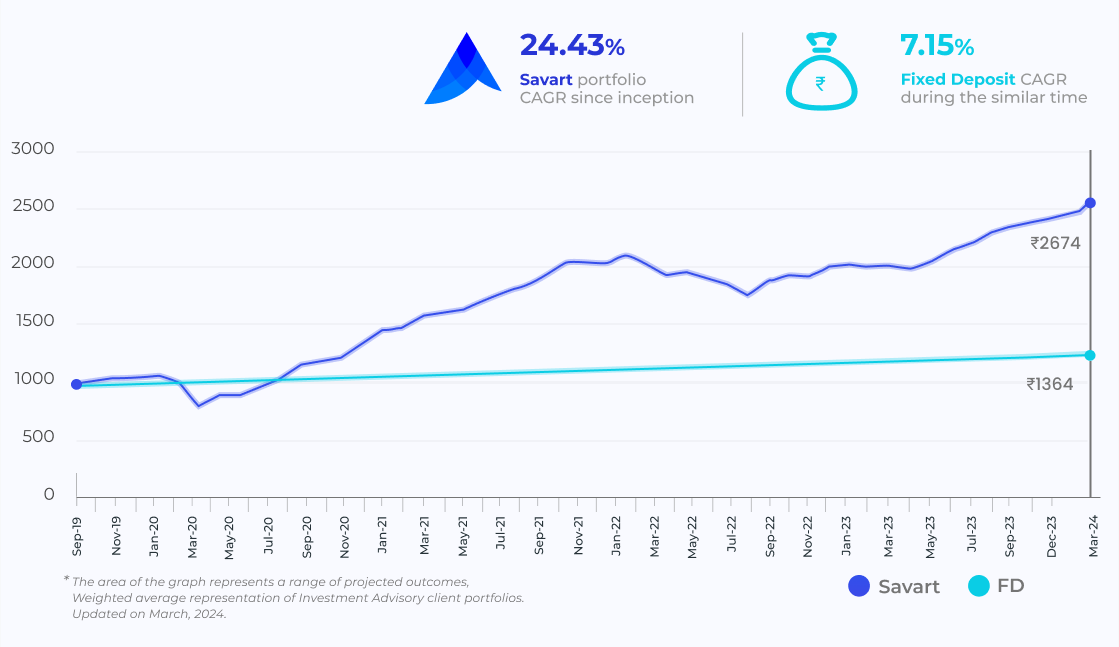
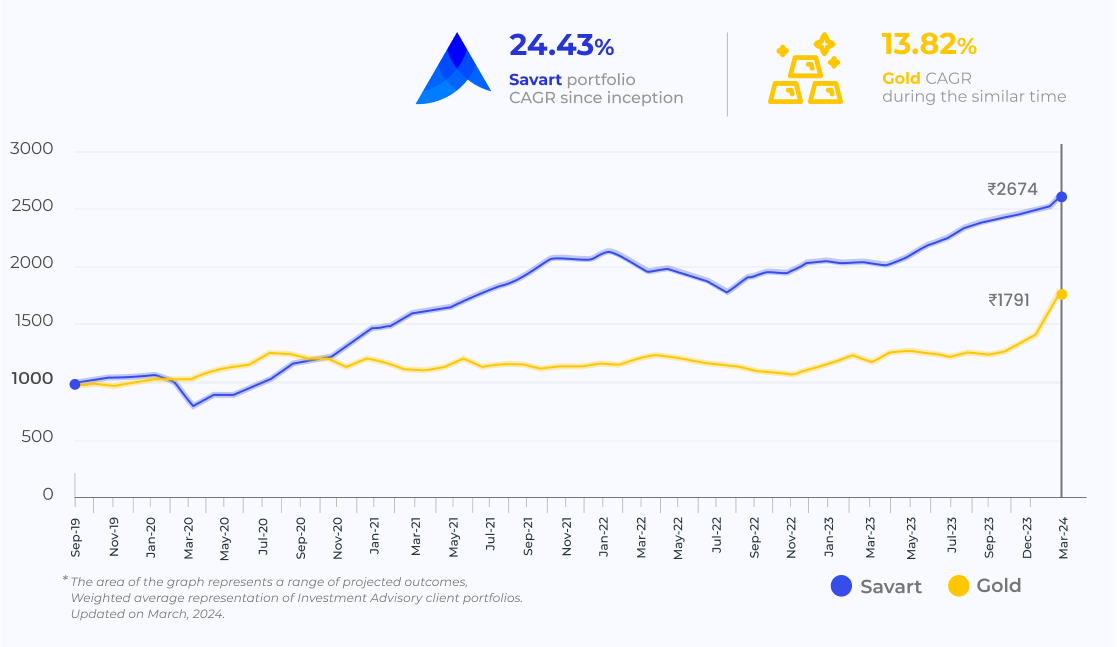
How Does Savart Work?

Investment Super App.
Savart is an end-to-end Investment solution. From goal-setting to investment advice, and from trade execution to portfolio tracking, we offer it all.
Global Opportunities
Whether it is a thriving pharma company in Toronto, an electric powerhouse in New York, or a tech startup in Bangalore–nothing misses our radar!

AI and Human Expertise
Experience the power of cutting-edge AI-technology, combined with patient, ethical and inclusive investing.
Savart in
Numbers
- Clients from Countries 33+
- Assets Under Advisory ₹ 2100+ Cr
- Users 165000+
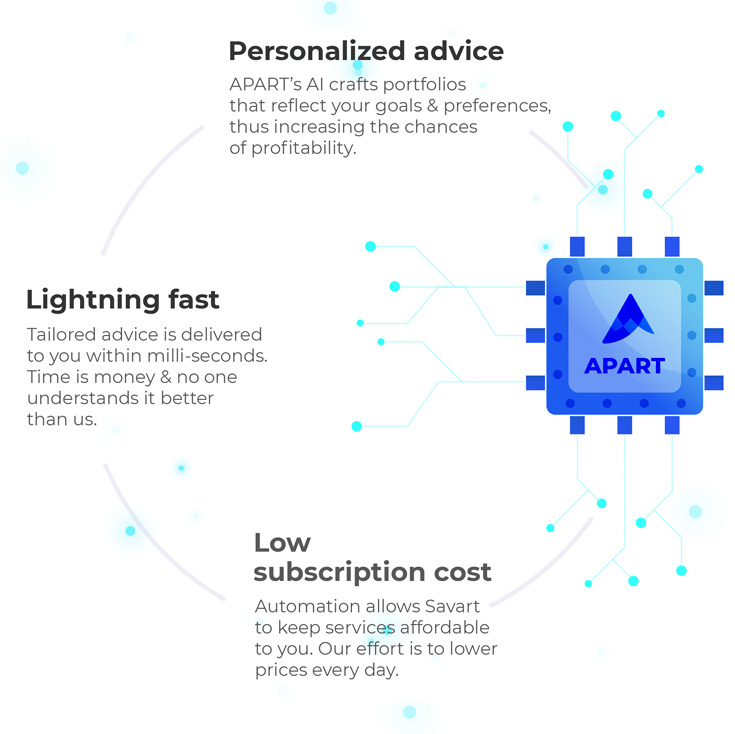
Advanced Process
Automation & Research Technology
APART AI automates research to increase investment performance.
Savart’s recommendation and research activities are driven by its AI-based system called APART (Advanced Process Automation & Research Technology). APART automates not just advice but also the underlying research, making it unique among peers. A traditional Robo-advisor automates the ‘advisory process’ using a set of rules input directly or indirectly by a human analyst. On the contrary, APART controls the end-to-end process with its three sub-systems Know More .
Our Clients Speak

Thiyagarajan
IT Professional

Chandra Sekar
Businessman, Muscat

Rashika Reddy
Doctor

Ravi Kumar
Geologist

Rajendra Shandilya
Retired Businessman

Poorna Chandra
Software Professional

Prashanth Appala
Doctor

Kashish Suneja
Software Engineer








Need Help?
Chat with us now or call on +91 90520 12341
Request a Call
Enter mobile number
Savart in Media
Our Subscription plan will help you realize your financial dreams
- 24 investment advices per year from our AI system
- Goal-based wealth planning
- Customize your investments based on personal beliefs
- 4 security reviews from your personal (non-Savart) portfolio
- Advice on high-performance stocks, mutual funds and bonds
- Ability to invest in India, USA and Canadian markets
- Phone/Email/Chat support
x
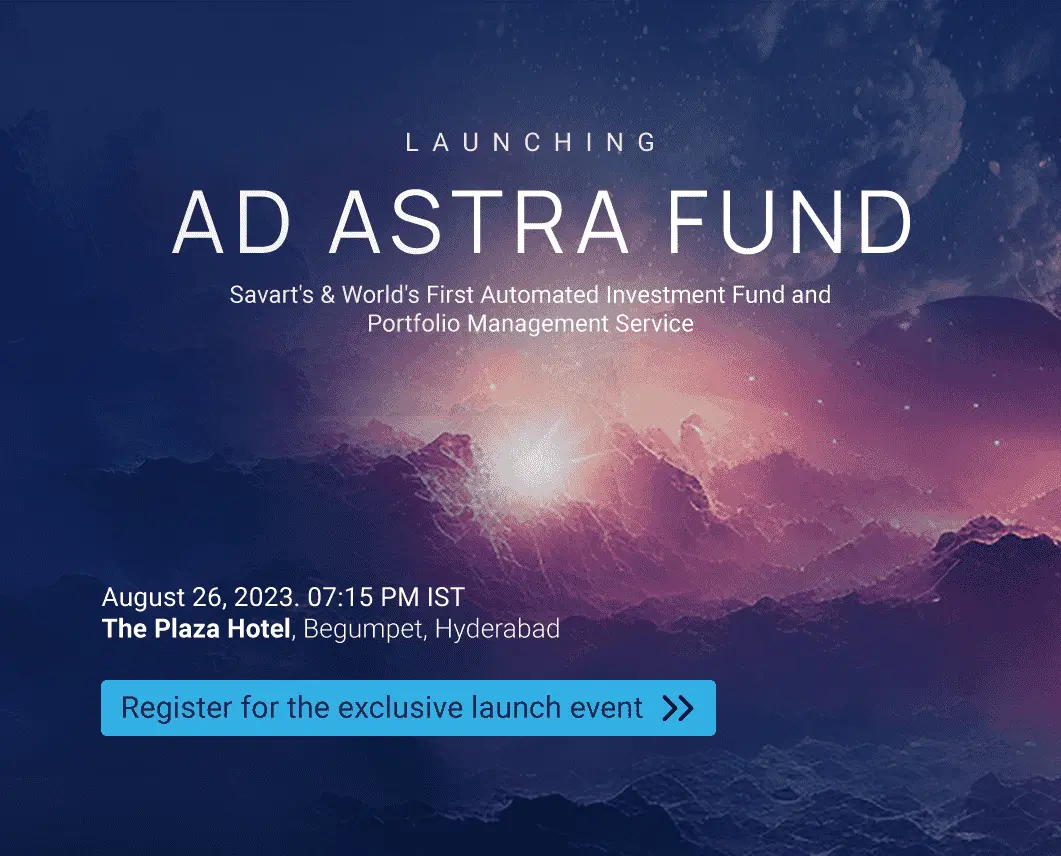

Savart is India’s largest Investment Advisor based on number of unique portfolios under advisory.









 4.7
4.7








